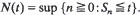First-passage times (FPTs) of two-dimensional Brownian motion have many applications in quantitative finance. However, despite various attempts since the 1960s, there are few analytical solutions available. By solving a nonhomogeneous modified Helmholtz equation in an infinite wedge, we find analytical solutions for the Laplace transforms of FPTs; these Laplace transforms can be inverted numerically. The FPT problems lead to a class of bivariate exponential distributions which are absolute continuous but do not have the memoryless property. We also prove that the density of the absolute difference of FPTs tends to ∞ if and only if the correlation between the two Brownian motions is positive.

The purpose of this paper is to study ageing properties of first-passage times of increasing Markov chains. We extend the literature to some new ageing classes, such as the IFR(2), NBU(2), DRLLt and NBULt classes. We also give sufficient conditions in the finite case, that are more efficient computationally, just in terms of the transition matrix K, in the discrete case, or the generator matrix Q, in the continuous case. For the uniformizable, continuous-time Markov processes, we derive conditions in terms of the discrete uniformized Markov chain for the NBU(2) and the NBULt classes. In the last section, a review of the main results in this direction in the literature is given, and we compare some of the conditions stated in this paper with others given in the literature about some other ageing classes. Some examples where these results are applied are given.

Using a matrix approach we discuss the first-passage time of a Markov process to exceed a given threshold or for the maximal increment of this process to pass a certain critical value. Conditions under which this first-passage time possesses various ageing properties are studied. Some results previously obtained by Li and Shaked (1995) are extended.

In this paper we investigate operators that map one or more probability distributions on the positive real line into another via their Laplace–Stieltjes transforms. Our goal is to make it easier to construct new transforms by manipulating known transforms. We envision the results here assisting modelling in conjunction with numerical transform inversion software. We primarily focus on operators related to infinitely divisible distributions and Lévy processes, drawing upon Feller (1971). We give many concrete examples of infinitely divisible distributions. We consider a cumulant-moment-transfer operator that allows us to relate the cumulants of one distribution to the moments of another. We consider a power-mixture operator corresponding to an independently stopped Lévy process. The special case of exponential power mixtures is a continuous analog of geometric random sums. We introduce a further special case which is remarkably tractable, exponential mixtures of inverse Gaussian distributions (EMIGs). EMIGs arise naturally as approximations for busy periods in queues. We show that the steady-state waiting time in an M/G/1 queue is the difference of two EMIGs when the service-time distribution is an EMIG. We consider several transforms related to first-passage times, e.g. for the M/M/1 queue, reflected Brownian motion and Lévy processes. Some of the associated probability density functions involve Bessel functions and theta functions. We describe properties of the operators, including how they transform moments.

Quasi-birth-death processes are commonly used Markov chain models in queueing theory, computer performance, teletraffic modeling and other areas. We provide a new, simple algorithm for the matrix-geometric rate matrix. We demonstrate that it has quadratic convergence. We show theoretically and through numerical examples that it converges very fast and provides extremely accurate results even for almost unstable models.

In this paper, we study the new better than used in expectation (NBUE) and new worse than used in expectation (NWUE) properties of Markov renewal processes. We show that a Markov renewal process belongs to a more general class of stochastic processes encountered in reliability or maintenance applications. We present sufficient conditions such that the first-passage times of these processes are new better than used in expectation. The results are applied to the study of shock and repair models, random repair time processes, inventory, and queueing models.

First it is shown that any generalized inverse of the infinitesimal generator of an irreducible Markov chain can be used to compute the exact stationary distribution and all the expected first-passage times of the chain. In the special case of a single-server queue this allows all computations to be done with upper-triangular matrices.

Next it is shown that the effect of a perturbation of the infinitesimal generator on the stationary distribution and expected first-passage times can also be computed using generalized inverses. These results extend and generalize Schweitzer's [9] original work using fundamental matrices. It is then shown that any perturbation can be broken up into a series of perturbations each involving a single state.

Electric water heating loads, in power systems, can be adequately modeled by Markov processes comprising a mix of continuous and discrete states. A physically-based characterization of the dynamic behavior of large aggregates of electric water heating loads is obtained by deriving the forward Kolmogorov equations associated with the individual hybrid-state processes. In addition, by focusing on the discrete part of the state, a Markov renewal viewpoint of the processes is developed. Both viewpoints are used to analyze and predict the transient and steady-state behavior of these loads, of great importance in load management applications.

We show that a theory for stopped two-dimensional random walks is well suited to describe cumulative shock models. Limit theorems for the lifetime/failure time of a system are provided.

Consider a device that deteriorates in time according to an increasing Markov process so that it fails as soon as a critical threshold is exceeded. NBUE and NWUE properties of the lifetime of the device are identified to extend the existing literature on the PFr, IFR, IFRA, and NBU cases. In particular, it is shown that NBUE and NWUE characterizations can be made through a monotonicity property on the potential operator of the Markov process.

We verify and extend a conjecture of Purdue (1981) concerning the stochastic monotonicity of absorption times in a class of compartmental urn models. We also describe the effect of increased variability in the reinforcement sizes. Finally, we investigate variability in the content process for large populations. In many applications, compartmental models substantially under-represent the variability observed in the data, so that there has been considerable interest in modifying the model to increase the variability. We show that the squared coefficient of variation of the content is not asymptotically negligible when both the size and the variability of the reinforcements are of the same order as the initial population.

Let (X0, Y0), (X1, Y1), · ·· be a sequence of independent two-dimensional random vectors such that (X1, Y1), (X2, Y2), · ·· are i.i.d. Let {(Sn, Un)}n≧0 be the associated sum process, and define for t ≧ 0 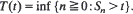Under suitable conditions on (X0, Y0) and (X1, Y1) we derive expansions up to vanishing terms, as t→∞, for EUT(t), Var UT(t) and Cov (UT(t), T(t)). Corresponding results will be obtained for EUN(t), Var UN(t) and Cov (UN(t), N(t)) when X0, Χ1 are both almost surely non-negative and

This paper shows how the Laplace transform analysis of Bailey (1954), (1957) can be continued to yield additional insights about the time-dependent behavior of the queue-length process in the M/M/1 model. A transform factorization is established that leads to a decomposition of the first moment as a function of time into two monotone components. This factorization facilitates developing approximations for the moments and determining their asymptotic behavior as . All descriptions of the transient behavior are expressed in terms of basic building blocks such as the first-passage-time distributions. The analysis is facilitated by appropriate scaling of space and time so that regulated or reflected Brownian motion (RBM) appears as the special case in which the traffic intensity ρ equals the critical value 1. An operational calculus is developed for obtaining M/M/1 results directly from corresponding RBM results as well as vice versa. The analysis thus provides useful insight about RBM approximations for queues.

A natural model for stochastic flow systems is regulated or reflecting Brownian motion (RBM), which is Brownian motion on the positive real line with constant negative drift and constant diffusion coefficient, modified by an impenetrable reflecting barrier at the origin. As a basis for understanding how stochastic flow systems approach steady state, this paper provides relatively simple descriptions of the moments of RBM as functions of time. In Part I attention is restricted to the case in which RBM starts at the origin; then the moment functions are increasing. After normalization by the steady-state limits, these moment c.d.f.&s (cumulative distribution functions) coincide with gamma mixtures of inverse Gaussian c.d.f.&s. The first moment c.d.f. thus coincides with the first-passage time to the origin starting in steady state with the exponential stationary distribution. From this probabilistic characterization, it follows that the kth-moment c.d.f is the k-fold convolution of the first-moment c.d.f. As a consequence, it is easy to see that the (k + 1)th moment approaches its steady-state limit more slowly than the kth moment. It is also easy to derive the asymptotic behavior as t →∞. The first two moment c.d.f.&s have completely monotone densities, supporting approximation by hyperexponential (H2) c.d.f.&s (mixtures of two exponentials). The H2 approximations provide easily comprehensible descriptions of the first two moment c.d.f.&s suitable for practical purposes. The two exponential components of the H2 approximation yield simple exponential approximations in different regimes. On the other hand, numerical comparisons show that the limit related to the relaxation time does not predict the approach to steady state especially well in regions of primary interest. In Part II (Abate and Whitt (1987a)), moments of RBM with non-zero initial conditions are treated by representing them as the difference of two increasing functions, one of which is the moment function starting at the origin studied here.

In this paper we define and analyze a class of cumulative shock models associated with a bivariate sequence {Xn, Yn}∞n=0 of correlated random variables. The {Xn} denote the sizes of the shocks and the {Yn} denote the times between successive shocks. The system fails when the cumulative magnitude of the shocks exceeds a prespecified level z. Two models, depending on whether the size of the nth shock is correlated with the length of the interval since the last shock or with the length of the succeeding interval until the next shock, are considered. Various transform results and asymptotic properties of the system failure time are obtained. Further, sufficient conditions are established under which system failure time is new better than used, new better than used in expectation, and harmonic new better than used in expectation.

An efficient computational approach to the analysis of finite birth-and-death models in a Markovian environment is given. The emphasis is upon obtaining numerical methods for evaluating stationary distributions and moments of first-passage times.

Let N(t) be a birth-death process on N = {0,1,2,· ··} governed by the transition rates λn > 0 (n ≧ 0) and μ η > 0 (n ≧ 1). Let mTm be the conditional first-passage time from r to n, given no visit to m where m <r < n. The downward conditional first-passage time nTm is defined similarly. It will be shown that , for any λn > 0 and μ η > 0. The limiting behavior of is considerably different from that of the ordinary first-passage time where, under certain conditions, exponentiality sets in as n →∞. We will prove that, when λn → λ > 0 and μ η → μ > 0 as n → ∞with ρ = λ /μ < 1, one has as r → ∞where TBP(λ,μ) is the server busy period of an M/M/1 queueing system with arrival rate λand service rate μ.

Let X1, X2, · ·· be a sequence of independent, identically distributed (i.i.d.) random variables with positive mean. An analogue of Rényi's (1962) stochastic geyser problem is solved for the associated process of first-passage times. More precisely, it is shown that a single realization of the sequence determines the distribution function (d.f.) of the Xn's almost surely (a.s.), even if the observations are erroneous up to an order o(log n).

Equivalence of rates of convergence in the central limit theorem between the vector of maximum sums and the corresponding first-passage variables is established. The bivariate case is studied. Analogous results about the equivalence between the vector of partial sums and corresponding renewal variables are also given and as a consequence we obtain a generalization of a theorem of Hunter (1974). Extension of the main result to more general first-passage times is also developed.

This paper describes an accurate method of approximating the mean of the first-passage time distribution for an Ornstein-Uhlenbeck process with a single absorbing barrier. The accuracy of the approximation is demonstrated through some numerical comparisons.