We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we introduce the transformed two-parameter Poisson–Dirichlet distribution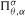 
on the ordered infinite simplex. Furthermore, we prove the central limit theorem related to this distribution when both the mutation rate θ and the selection rate σ become large in a specified manner. As a consequence, we find that the properly scaled homozygosities have asymptotical normal behavior. In particular, there is a certain phase transition with the limit depending on the relative strength of σ and θ.
