1 results
On queueing systems with renewal departure processes
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 3 / September 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 657-673
- Print publication:
- September 1983
-
- Article
- Export citation
-
It is proved that, for a large class of stable stationary queueing systems with renewal arrival processes and without losses, a necessary condition for the departure process also to be a renewal process is that its interval distribution be the same as that of the arrival process. This result is then applied to the classical GI/G/s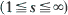
queueing systems. In particular, alternative proofs of known characterizations of the M/G/1 and GI/M/1 systems are given, as well as a characterization of the GI/G/∞ system. In the course of the proofs, sufficient conditions for the existence of all the moments of the stationary queue-size distributions of both the GI/G/1 and GI/G/∞ systems are derived.
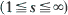queueing systems. In particular, alternative proofs of known characterizations of the 