1 results
AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 242-253
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
For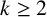
$k\geq 2$ and a nonzero integer n, a generalised Diophantine m-tuple with property 
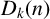$D_k(n)$ is a set of m positive integers 
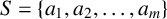$S = \{a_1,a_2,\ldots , a_m\}$ such that 
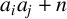$a_ia_j + n$ is a kth power for 
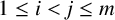$1\leq i< j\leq m$. Define 
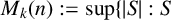$M_k(n):= \text {sup}\{|S| : S$ having property 
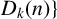$D_k(n)\}$. Dixit et al. [‘Generalised Diophantine m-tuples’, Proc. Amer. Math. Soc. 150(4) (2022), 1455–1465] proved that 
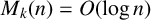$M_k(n)=O(\log n)$, for a fixed k, as n varies. In this paper, we obtain effective upper bounds on 
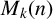$M_k(n)$. In particular, we show that for 
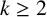$k\geq 2$, 
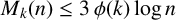$M_k(n) \leq 3\,\phi (k) \log n$ if n is sufficiently large compared to k.
