For a general autonomous planar polynomial differential system, it is difficult to find conditions that are easy to verify and which guarantee global asymptotic stability, weakening the Markus–Yamabe condition. In this paper, we provide three conditions that guarantee the global asymptotic stability for polynomial differential systems of the form 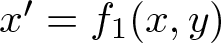$x^{\prime}=f_1(x,y)$, 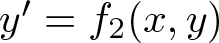$y^{\prime}=f_2(x,y)$, where f1 has degree one, f2 has degree 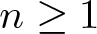$n\ge 1$ and has degree one in the variable y. As a consequence, we provide sufficient conditions, weaker than the Markus–Yamabe conditions that guarantee the global asymptotic stability for any generalized Liénard polynomial differential system of the form 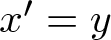$x^{\prime}=y$, 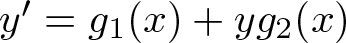$y^{\prime}=g_1(x) +y g_2(x)$ with g1 and g2 polynomials of degrees n and m, respectively.

The article proposes a nonlinear optimal (H-infinity) control approach for a type of underactuated power-line inspection robots. To implement this control scheme, the state-space model of the power-line inspection robots undergoes first approximate linearization around a temporary operating point, through first-order Taylor series expansion and through the computation of the associated Jacobian matrices. To select the feedback gains of the controller an algebraic Riccati equation is solved at each time step of the control method. The global stability properties of the control loop are proven through Lyapunov analysis. The significance of the article’s results is outlined in the following: (i) the proposed control method is suitable for treating underactuated robotic systems and in general nonlinear dynamical systems with control inputs gain matrices which are in a nonquadratic form, (ii) by achieving stabilization of the power-line inspection robots in underactuation conditions the proposed control method ensures the reliable functioning of these robotic systems in the case of actuators’ failures or enables the complete removal of certain actuators and the reduction of the weight of these robotic systems, (iii) the proposed control method offers a solution to the nonlinear optimal control problem which is of proven global stability while also remaining computationally tractable, (iv) the proposed nonlinear optimal control method retains the advantages of linear optimal control that is fast and accurate tracking of reference setpoints under moderate variations of the control inputs, and (v) by minimizing the amount of energy that is dispersed by the actuators of the power-line inspection robots the proposed control method improves the autonomy and operational capacity of such robotic systems.

In this paper we propose new tuning conditions for three saturated nonlinear proportional-integral-derivative (PID) global regulators with bounded torques for robot manipulators, which have been presented previously in the literature. The motivation of this work relies on the fact that the tuning conditions presented previously in the literature for assuring global asymptotic stability are so restrictive that it had been impossible, until now, to carry out experimental tests. New tuning criteria of unsaturated PID controllers for robot manipulators with stability conditions more relaxed than those presented previously in the literature have been proposed recently in some works by the authors. This was achieved by setting the stability conditions as expressions that have to be satisfied at each joint instead of general conditions for the whole robot. Based on this idea, we now obtain stability conditions for saturated global PID controllers which are so relaxed that they have allowed to perform, by the first time, experimental tests using controller gains which completely satisfy the proposed stability conditions. The results of such experiments are presented in this paper, where we have used a two-degrees-of-freedom robot manipulator.

We investigate the global asymptotic stability for positive solutions to a class of general symmetric rational difference equations and prove that the unique positive equilibrium 1 of the general symmetric rational difference equations is globally asymptotically stable. As a special case of our result, we solve the conjecture raised by Berenhaut, Foley and Stević [‘The global attractivity of the rational difference equation yn=(yn−k+yn−m)/(1+yn−kyn−m)’, Appl. Math. Lett.20 (2007), 54–58].