1 results
A WALK WITH GOODSTEIN
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-19
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
Goodstein’s principle is arguably the first purely number-theoretic statement known to be independent of Peano arithmetic. It involves sequences of natural numbers which at first appear to diverge, but eventually decrease to zero. These sequences are defined relative to a notation system based on exponentiation for the natural numbers. In this article, we provide a self-contained and modern analysis of Goodstein’s principle, obtaining some variations and improvements. We explore notions of optimality for notation systems and apply them to the classical Goodstein process and to a weaker variant based on multiplication rather than exponentiation. In particular, we introduce the notion of base-change maximality, and show how it leads to far-reaching extensions of Goodstein’s result. We moreover show that by varying the initial base of the Goodstein process, one readily obtains independence results for each of the fragments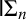
$\mathsf {I}\Sigma _n$ of Peano arithmetic.
