We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this note, we present examples of non-quasi-geodesic metric spaces which are hyperbolic (i.e., satisfying Gromov’s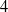 
$4$-point condition) while the intersection of any two metric balls therein does not either ‘look like’ a ball or has uniformly bounded eccentricity. This answers an open question posed by Chatterji and Niblo.
