The system of mating that maintains a general genotypic distribution among females with respect to an X-linked locus is defined. In particular, it is shown that Hardy–Weinberg proportions can be maintained with non-random mating.

G. H. Hardy (1877–1947) and Wilhelm Weinberg (1862–1937) had very different lives, but in the minds of geneticists, the two are inextricably linked through the ownership of an apparently simple law called the Hardy–Weinberg law. We demonstrate that the simplicity is more apparent than real. Hardy derived the well-known trio of frequencies {q2, 2pq, p2} with a concise demonstration, whereas for Weinberg it was the prelude to an ingenious examination of the inheritance of twinning in man. Hardy's recourse to an identity relating to the distribution of types among offspring following random mating, rather than an identity relating to the mating matrix, may be the reason why he did not realize that Hardy–Weinberg equilibrium can be reached and sustained with non-random mating. The phrase ‘random mating’ always comes up in reference to the law. The elusive nature of this phrase is part of the reason for the misunderstandings that occur but also because, as we explain, mathematicians are able to use it in a different way from the man-in-the-street. We question the unthinking appeal to random mating as a model and explanation of the distribution of genotypes even when they are close to Hardy–Weinberg proportions. Such sustained proportions are possible under non-random mating.

For N = 1, 2, …, let {(XN (k), YN (k)), k = 0, 1, …} be a time-homogeneous Markov chain in 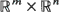. Suppose that, asymptotically as N → ∞, the ‘infinitesimal' covariances and means of XN([·/ε N]) are aij(x, y) and bi(x, y), and those of YN ([·/δ N]) are 0 and cl(x, y). Assume 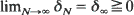and limN→∞ε N/δ N = 0. Then, under a global asymptotic stability condition on dy/dt = c(x, y) or a related difference equation (and under some technical conditions), it is shown that (i) XN([·/ε N]) converges weakly to a diffusion process with coefficients aij(x, 0) and bi(x, 0) and (ii) YN([t/ε N]) → 0 in probability for every t > 0. The assumption in Ethier and Nagylaki (1980) that the processes are uniformly bounded is removed here.

The results are used to establish diffusion approximations of multiallelic one-locus stochastic models for mutation, selection, and random genetic drift in a finite, panmictic, diploid population. The emphasis is on rare, severely deleterious alleles. Models with multinomial sampling of genotypes in the monoecious, dioecious autosomal, and X-linked cases are analyzed, and an explicit formula for the stationary distribution of allelic frequencies is obtained.