1 results
Conjugacy Classes and Binary Quadratic Forms for the Hecke Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 570-583
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
-
In this paper we give a lower bound with respect to block length for the trace of non-elliptic conjugacy classes of the Hecke groups. One consequence of our bound is that there are finitely many conjugacy classes of a given trace in anyHecke group. We show that another consequence of our bound is that class numbers are finite for related hyperbolic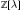
$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms. We give canonical class representatives and calculate class numbers for some classes of hyperbolic 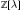$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms.
