We present a combinatorial proof for the existence of the sign-refined grid homology in lens spaces and a self-contained proof that 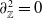 $\partial _{\mathbb{Z}}^2 = 0$. We also present a Sage programme that computes
$\partial _{\mathbb{Z}}^2 = 0$. We also present a Sage programme that computes  $\widehat{\mathrm{GH}} (L(p,q),K;\mathbb{Z})$ and provide empirical evidence supporting the absence of torsion in these groups.
$\widehat{\mathrm{GH}} (L(p,q),K;\mathbb{Z})$ and provide empirical evidence supporting the absence of torsion in these groups.
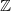 $\mathbb{Z}$ coefficients and computations
$\mathbb{Z}$ coefficients and computations