1 results
A Semilinear Problem for the Heisenberg Laplacian on Unbounded Domains
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 6 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1279-1290
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
-
We study the semilinear equation
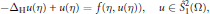$$-{{\Delta }_{\mathbb{H}}}u(\eta )\,+\,u(\eta )\,=\,f(\eta ,\,\,u(\eta )),\,u\in \,\overset{\circ }{\mathop{S}}\,_{1}^{2}(\Omega ),$$where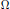
$\Omega $ is an unbounded domain of the Heisenberg group 
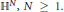${{\mathbb{H}}^{N}},\,N\,\ge \,1$. The space 
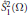$\overset{\circ }{\mathop{S}}\,_{1}^{2}(\Omega )$ is the Heisenberg analogue of the Sobolev space 
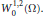$W_{0}^{1,\,2}\,\left( \Omega \right)$. The function 
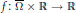$f\,:\,\overset{-}{\mathop{\Omega }}\,\,\times \,\mathbb{R}\,\to \,\mathbb{R}$ is supposed to be odd in 
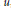$u$, continuous and satisfy some (superlinear but subcritical) growth conditions. The operator 
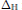${{\Delta }_{\mathbb{H}}}$ is the subelliptic Laplacian on the Heisenberg group. We give a condition on 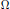$\Omega $ which implies the existence of infinitely many solutions of the above equation. In the proof we rewrite the equation as a variational problem, and show that the corresponding functional satisfies the Palais–Smale condition. This might be quite surprising since we deal with domains which are far frombounded. The technique we use rests on a compactness argument and the maximum principle.
