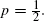We consider a sequence of random graphs constructed by a hierarchical procedure. The construction replaces existing edges by pairs of edges in series or parallel with probability p. We investigate the effective resistance across the graphs, first-passage percolation on the graphs and the Cheeger constants of the graphs as the number of edges tends to infinity. In each case we find a phase transition at