We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we study asymptotic behaviour of distributed parameter systems governedby partial differential equations (abbreviated to PDE). We first review some recently developed resultson the stability analysis of PDE systems by Lyapunov's second method. On constructing Lyapunov functionalswe prove next an asymptotic exponential stability result for a class of symmetric hyperbolic PDEsystems. Then we apply the result to establish exponential stability of various chemical engineeringprocesses and, in particular, exponential stability of heat exchangers. Through concrete examples weshow how Lyapunov's second method may be extended to stability analysis of nonlinear hyperbolic PDE.Meanwhile we explain how the method is adapted to the framework of Banach spaces Lp , $1<p\leq \infty$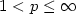 
.
