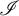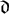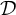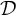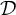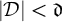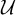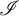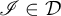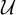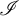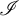We give a new characterization of the cardinal invariant 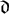 \mathfrak {d} as the minimal cardinality of a family
\mathfrak {d} as the minimal cardinality of a family 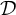 \mathcal {D} of tall summable ideals such that an ultrafilter is rapid if and only if it has non-empty intersection with all the ideals in the family
\mathcal {D} of tall summable ideals such that an ultrafilter is rapid if and only if it has non-empty intersection with all the ideals in the family 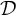 \mathcal {D}. On the other hand, we prove that in the Miller model, given any family
\mathcal {D}. On the other hand, we prove that in the Miller model, given any family 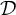 \mathcal {D} of analytic tall p-ideals such that
\mathcal {D} of analytic tall p-ideals such that 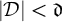 \vert \mathcal {D}\vert <\mathfrak {d}, there is an ultrafilter
\vert \mathcal {D}\vert <\mathfrak {d}, there is an ultrafilter 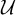 \mathcal {U} which is an
\mathcal {U} which is an 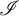 \mathscr {I}-ultrafilter for all ideals
\mathscr {I}-ultrafilter for all ideals 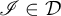 \mathscr {I}\in \mathcal {D} at the same time, yet
\mathscr {I}\in \mathcal {D} at the same time, yet 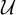 \mathcal {U} is not a rapid ultrafilter. As a corollary, we obtain that in the Miller model, given any analytic tall p-ideal
\mathcal {U} is not a rapid ultrafilter. As a corollary, we obtain that in the Miller model, given any analytic tall p-ideal 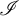 \mathscr {I},
\mathscr {I}, 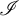 \mathscr {I}-ultrafilters are dense in the Rudin–Blass ordering, generalizing a theorem of Bartoszyński and S. Shelah, who proved that in such model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering. This theorem also shows some limitations about possible generalizations of a theorem of C. Laflamme and J. Zhu.
\mathscr {I}-ultrafilters are dense in the Rudin–Blass ordering, generalizing a theorem of Bartoszyński and S. Shelah, who proved that in such model, Hausdorff ultrafilters are dense in the Rudin–Blass ordering. This theorem also shows some limitations about possible generalizations of a theorem of C. Laflamme and J. Zhu.