Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Last 3 years (1)

From year:

To year:

Apply

Mathematics (1)

in-pairs

Ergodic Theory and Dynamical Systems (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Measure-theoretic sequence entropy pairs and mean sensitivity
Part of
- Ergodic theory
- Topological dynamics
FELIPE GARCÍA-RAMOS, VÍCTOR MUÑOZ-LÓPEZ
Journal:

Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024

Published online by Cambridge University Press:

19 September 2023, pp. 1531-1540

Print publication:

June 2024
- Article
- - You have access
- PDF
- HTML
- Export citation
We characterize measure-theoretic sequence entropy pairs of continuous actions of abelian groups using mean sensitivity. This addresses an open question of Li and Yu [On mean sensitive tuples. J. Differential Equations 297 (2021), 175–200]. As a consequence of our results, we provide a simpler characterization of Kerr and Li’s independence sequence entropy pairs (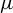$\mu $-IN-pairs) when the measure is ergodic and the group is abelian.