Refine search
Actions for selected content:
1 results
Zero-temperature ising spin dynamics on the homogeneous tree of degree three
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 3 / September 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 736-747
- Print publication:
- September 2000
-
- Article
- Export citation
 infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θ
infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θ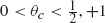 spin chains almost surely never form for
spin chains almost surely never form for 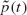 that any particular vertex changes spin after time
that any particular vertex changes spin after time 