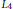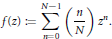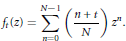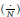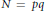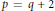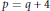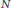1 results
Merit Factors of Polynomials Formed by Jacobi Symbols
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 1 / 01 February 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-50
- Print publication:
- 01 February 2001
-
- Article
-
- You have access
- Export citation
-
We give explicit formulas for the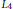
${{L}_{4}}$ norm (or equivalently for the merit factors) of various sequences of polynomials related to the polynomials
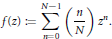$$f\left( z \right):=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n}{N} \right){{z}^{n}}.}$$and
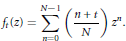$${{f}_{t}}(z)\,=\,\sum\limits_{n=0}^{N-1}{\left( \frac{n+t}{N} \right){{z}^{n}}.}$$where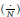
$\left( \frac{.}{N} \right)$ is the Jacobi symbol.Two cases of particular interest are when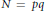
$N\,=\,pq$ is a product of two primes and 
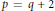$p\,=\,q\,+\,2$ or 
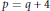$p\,=\,q\,+\,4$. This extends work of Høholdt, Jensen and Jensen and of the authors.This study arises from a number of conjectures of Erdős, Littlewood and others that concern the norms of polynomials with −1, 1 coefficients on the disc. The current best examples are of the above form when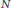
$N$ is prime and it is natural to see what happens for composite 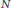$N$.
