In a paper by Badulescu [Global Jacquet–Langlands correspondence, multiplicity one and classification of automorphic representations, Invent. Math. 172 (2008), 383–438], results on the global Jacquet–Langlands correspondence, (weak and strong) multiplicity-one theorems and the classification of automorphic representations for inner forms of the general linear group over a number field were established, under the assumption that the local inner forms are split at archimedean places. In this paper, we extend the main local results of that article to archimedean places so that the above condition can be removed. Along the way, we collect several results about the unitary dual of general linear groups over ℝ, ℂ or ℍ which are of independent interest.
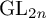 $\mathrm {GL}_{2n}$
OF UNITARY TYPE
$\mathrm {GL}_{2n}$
OF UNITARY TYPE