In the early 1980s, Johnson defined a homomorphism
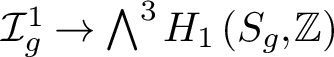 $\mathcal {I}_{g}^1\to \bigwedge ^3 H_1\left (S_{g},\mathbb {Z}\right )$
, where
$\mathcal {I}_{g}^1\to \bigwedge ^3 H_1\left (S_{g},\mathbb {Z}\right )$
, where
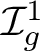 $\mathcal {I}_{g}^1$
is the Torelli group of a closed, connected, and oriented surface of genus g with a boundary component and
$\mathcal {I}_{g}^1$
is the Torelli group of a closed, connected, and oriented surface of genus g with a boundary component and
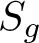 $S_g$
is the corresponding surface without a boundary component. This is known as the Johnson homomorphism.
$S_g$
is the corresponding surface without a boundary component. This is known as the Johnson homomorphism.
We study the map induced by the Johnson homomorphism on rational homology groups and apply it to abelian cycles determined by disjoint bounding-pair maps, in order to compute a large quotient of
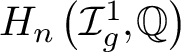 $H_n\left (\mathcal {I}_{g}^1,\mathbb {Q}\right )$
in the stable range. This also implies an analogous result for the stable rational homology of the Torelli group
$H_n\left (\mathcal {I}_{g}^1,\mathbb {Q}\right )$
in the stable range. This also implies an analogous result for the stable rational homology of the Torelli group
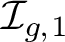 $\mathcal {I}_{g,1}$
of a surface with a marked point instead of a boundary component. Further, we investigate how much of the image of this map is generated by images of such cycles and use this to prove that in the pointed case, they generate a proper subrepresentation of
$\mathcal {I}_{g,1}$
of a surface with a marked point instead of a boundary component. Further, we investigate how much of the image of this map is generated by images of such cycles and use this to prove that in the pointed case, they generate a proper subrepresentation of
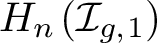 $H_n\left (\mathcal {I}_{g,1}\right )$
for
$H_n\left (\mathcal {I}_{g,1}\right )$
for
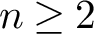 $n\ge 2$
and g large enough.
$n\ge 2$
and g large enough.