1 results
Galois-theoretic features for 1-smooth pro-p groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 525-541
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Let p be a prime. A pro-p group G is said to be 1-smooth if it can be endowed with a continuous representation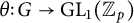
$\theta \colon G\to \mathrm {GL}_1(\mathbb {Z}_p)$
such that every open subgroup H of G, together with the restriction 
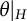$\theta \vert _H$
, satisfies a formal version of Hilbert 90. We prove that every 1-smooth pro-p group contains a unique maximal closed abelian normal subgroup, in analogy with a result by Engler and Koenigsmann on maximal pro-p Galois groups of fields, and that if a 1-smooth pro-p group is solvable, then it is locally uniformly powerful, in analogy with a result by Ware on maximal pro-p Galois groups of fields. Finally, we ask whether 1-smooth pro-p groups satisfy a “Tits’ alternative.”
