In this paper we investigate the potential of Lévy copulas as a tool for modelling dependence between compound Poisson processes and their applications in insurance. We analyse characteristics regarding the dependence in frequency and dependence in severity allowed by various Lévy copula models. Through the introduction of new Lévy copulas and comparison with the Clayton Lévy copula, we show that Lévy copulas allow for a great range of dependence structures.
Procedures for analysing the fit of Lévy copula models are illustrated by fitting a number of Lévy copulas to a set of real data from Swiss workers compensation insurance. How to assess the fit of these models with respect to the dependence structure exhibited by the dataset is also discussed.
Finally, we provide a decomposition of the trivariate compound Poisson process and discuss how trivariate Lévy copulas model dependence in this multivariate setting.

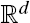 with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called
with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called 