1 results
Simultaneous deformations and Poisson geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 04 May 2015, pp. 1763-1790
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
-
We consider the problem of deforming simultaneously a pair of given structures. We show that such deformations are governed by an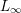
$L_{\infty }$-algebra, which we construct explicitly. Our machinery is based on Voronov’s derived bracket construction. In this paper we consider only geometric applications, including deformations of coisotropic submanifolds in Poisson manifolds, of twisted Poisson structures, and of complex structures within generalized complex geometry. These applications cannot be, to our knowledge, obtained by other methods such as operad theory.
