In this paper the germ of neighborhood of a compact leaf in a Lagrangian foliation is symplectically classified when the compact leaf is 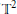 ${{\mathbb{T}}^{2}}$, the affine structure induced by the Lagrangian foliation on the leaf is complete, and the holonomy of
${{\mathbb{T}}^{2}}$, the affine structure induced by the Lagrangian foliation on the leaf is complete, and the holonomy of 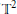 ${{\mathbb{T}}^{2}}$ in the foliation linearizes. The germ of neighborhood is classified by a function, depending on one transverse coordinate, this function is related to the affine structure of the nearly compact leaves.
${{\mathbb{T}}^{2}}$ in the foliation linearizes. The germ of neighborhood is classified by a function, depending on one transverse coordinate, this function is related to the affine structure of the nearly compact leaves.
