We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Consider a Lamperti–Kiu Markov additive process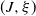 
$(J, \xi)$ on 
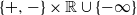$\{+, -\}\times\mathbb R\cup \{-\infty\}$, where J is the modulating Markov chain component. First we study the finiteness of the exponential functional and then consider its moments and tail asymptotics under Cramér’s condition. In the strong subexponential case we determine the subexponential tails of the exponential functional under some further assumptions.
