We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We find all integer solutions to the equation
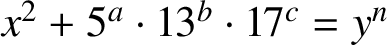$x^2+5^a\cdot 13^b\cdot 17^c=y^n$
with
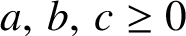$a,\,b,\,c\geq 0$
,
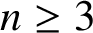$n\geq 3$
,
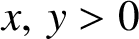$x,\,y>0$
and
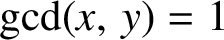$\gcd (x,\,y)=1$
. Our proof uses a deep result about primitive divisors of Lucas sequences in combination with elementary number theory and computer search.
