This essay discusses rules and semantic clauses relating to Substitution—Leibniz’s law in the conjunctive-implicational form 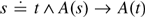 $s\dot{ = }t \wedge A\left( s \right) \to A\left( t \right)$—as these are put forward in Priest’s books In Contradiction and An Introduction to Non-Classical Logic: From If to Is. The stated rules and clauses are shown to be too weak in some cases and too strong in others. New ones are presented and shown to be correct. Justification for the various rules is probed and it is argued that Substitution ought to fail.
$s\dot{ = }t \wedge A\left( s \right) \to A\left( t \right)$—as these are put forward in Priest’s books In Contradiction and An Introduction to Non-Classical Logic: From If to Is. The stated rules and clauses are shown to be too weak in some cases and too strong in others. New ones are presented and shown to be correct. Justification for the various rules is probed and it is argued that Substitution ought to fail.