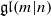This paper introduces type P web supercategories. They are defined as diagrammatic monoidal ${\mathbb {k}}$-linear supercategories via generators and relations. We study the structure of these categories and provide diagrammatic bases for their morphism spaces. We also prove these supercategories provide combinatorial models for the monoidal supercategory generated by the symmetric powers of the natural module and their duals for the Lie superalgebra of type P.

Let be a classical Lie superalgebra and let ℱ be the category of finite-dimensional -supermodules which are completely reducible over the reductive Lie algebra . In [B. D. Boe, J. R. Kujawa and D. K. Nakano, Complexity and module varieties for classical Lie superalgebras, Int. Math. Res. Not. IMRN (2011), 696–724], we demonstrated that for any module M in ℱ the rate of growth of the minimal projective resolution (i.e. the complexity of M) is bounded by the dimension of . In this paper we compute the complexity of the simple modules and the Kac modules for the Lie superalgebra . In both cases we show that the complexity is related to the atypicality of the block containing the module.

In this paper we discuss the simplicity criteria of (−1,−1)-Freudenthal Kantor triple systems and give examples of such triple systems, from which we can construct some Lie superalgebras. We also show that we can associate a Jordan triple system to any (ε,δ)-Freudenthal Kantor triple system. Further, we introduce the notion of δ-structurable algebras and connect them to (−1,δ)-Freudenthal Kantor triple systems and the corresponding Lie (super)algebra construction.

We have constructed Lie superalgebras $D(2,1;\alpha)$, $G(3)$ and $F(4)$ from $U(-1,-1)$-balanced Freudenthal–Kantor triple systems in a natural way.

AMS 2000 Mathematics subject classification: Primary 17A40; 17B60

Let $\Gamma$ be a countable abelian semigroup and $\mathcal{A}$ be a countable abelian group satisfying a certain finiteness condition. Suppose that a group $G$ acts on a $(\Gamma \times \mathcal{A})$-graded Lie superalgebra $\mathfrak{L} =\bigoplus_{(\alpha, a) \Gamma \times \mathcal{A}} \mathfrak{L}_{(\alpha, a)}$ by Lie superalgebra automorphisms preserving the $(\Gamma \times \mathcal{A})$-gradation. In this paper, we show that the Euler--Poincar\'e principle yields the generalized denominator identity for $\mathfrak{L}$ and derive a closed form formula for the supertraces $\text{str}(g| \mathcal{L}_{(\alpha, a)})$ for all $g\in G$, where $(\alpha, a) \in \Gamma \times \mathcal{A}$. We discuss the applications of our supertrace formula to various classes of infinite-dimensional Lie superalgebras such as free Lie superalgebras and generalized Kac--Moody superalgebras. In particular, we determine the decomposition of free Lie superalgebras into a direct sum of irreducible $\text{GL}(n) \times \text{GL}(k)$-modules, and the supertraces of the Monstrous Lie superalgebras with group actions. Finally, we prove that the generalized characters of Verma modules and irreducible highest-weight modules over a generalized Kac--Moody superalgebra $\mathfrak{g}$ corresponding to the Dynkin diagram automorphism $\sigma$ are the same as the usual characters of Verma modules and irreducible highest-weight modules over the orbit Lie superalgebra $\breve{\mathfrak{g}} = \mathfrak{g}(\sigma)$ determined by $\sigma$. 1991 Mathematics Subject Classification: 17A70, 17B01, 17B65, 17B70, 11F22.