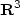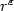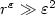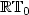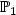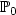Refine search
Actions for selected content:
15 results
Pressure live loads and the variational derivation of linear elasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1929-1964
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
14 - A Brief Introduction to Poroelasticity and Simulation of Coupled Geomechanics and Flow in MRST
- from Part III - Modeling of New Physical Processes
-
-
- Book:
- Advanced Modeling with the MATLAB Reservoir Simulation Toolbox
- Published online:
- 20 November 2021
- Print publication:
- 25 November 2021, pp 549-596
-
- Chapter
-
- You have access
- Open access
- Export citation
Spectral properties of the Neumann–Poincaré operator and cloaking by anomalous localized resonance for the elasto-static system
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 12 April 2017, pp. 189-225
-
- Article
- Export citation
Uniform Convergence Analysis of a Higher Order Hybrid Stress Quadrilateral Finite Element Method for Linear Elasticity Problems
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 399-425
- Print publication:
- June 2016
-
- Article
- Export citation
A Second Order Finite-Difference Ghost-Point Method for Elasticity Problems on Unbounded Domains with Applications to Volcanology
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 983-1009
- Print publication:
- October 2014
-
- Article
- Export citation
Relating phase field and sharp interface approaches tostructural topology optimization
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 05 August 2014, pp. 1025-1058
- Print publication:
- October 2014
-
- Article
- Export citation
Error estimates for the ultra weak variational formulation inlinear elasticity∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 August 2012, pp. 183-211
- Print publication:
- January 2013
-
- Article
- Export citation
Analyse d'un disque en compression diamétrale
-
- Journal:
- Mechanics & Industry / Volume 10 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 25 June 2009, pp. 61-65
- Print publication:
- January 2009
-
- Article
- Export citation
Singular Perturbations For Heart ImageSegmentation Tracking
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 4 / Issue 1 / 2009
- Published online by Cambridge University Press:
- 27 January 2009, pp. 183-194
- Print publication:
- 2009
-
- Article
- Export citation
Weak Formulations and Solution Multiplicityof Equilibrium Configurations with Coulomb Friction
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 4 / Issue 1 / 2009
- Published online by Cambridge University Press:
- 27 January 2009, pp. 147-162
- Print publication:
- 2009
-
- Article
- Export citation
Small amplitude homogenization applied to modelsof non-periodic fibrous materials
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 15 December 2007, pp. 1061-1087
- Print publication:
- November 2007
-
- Article
- Export citation
Junction of elastic plates and beams
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 3 / July 2007
- Published online by Cambridge University Press:
- 26 July 2007, pp. 419-457
- Print publication:
- July 2007
-
- Article
- Export citation
Analysis of a new augmented mixed finite element methodfor linear elasticity allowing $\mathbb{RT}_0$
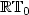 - $\mathbb{P}_1$
- $\mathbb{P}_1$ 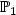 - $\mathbb{P}_0$
- $\mathbb{P}_0$ 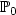 approximations
approximations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 1-28
- Print publication:
- January 2006
-
- Article
- Export citation
Generalized Newton methods for the 2D-Signorini contact problem with friction in function space
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 827-854
- Print publication:
- July 2005
-
- Article
- Export citation
Computation of 3D vertex singularities for linear elasticity: Error estimates for a finite element methodon graded meshes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1043-1070
- Print publication:
- November 2002
-
- Article
- Export citation