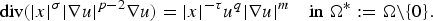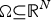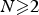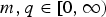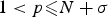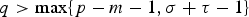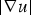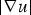1 results
Gradient estimates for nonlinear elliptic equations with a gradient-dependent nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1361-1376
- Print publication:
- June 2020
-
- Article
- Export citation
-
In this paper, we obtain gradient estimates of the positive solutions to weighted p-Laplacian type equations with a gradient-dependent nonlinearity of the form 0.1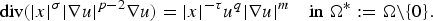
Here,
$${\rm div }( \vert x \vert ^\sigma \vert \nabla u \vert ^{p-2}\nabla u) = \vert x \vert ^{-\tau }u^q \vert \nabla u \vert ^m\quad {\rm in}\;\Omega^*: = \Omega {\rm \setminus }\{ 0\} .$$
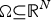$\Omega \subseteq {\open R}^N$ denotes a domain containing the origin with 
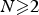$N\ges 2$, whereas 
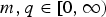$m,q\in [0,\infty )$, 
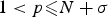$1<p\les N+\sigma $ and 
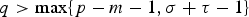$q>\max \{p-m-1,\sigma +\tau -1\}$. The main difficulty arises from the dependence of the right-hand side of (0.1) on x, u and 
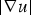$ \vert \nabla u \vert $, without any upper bound restriction on the power m of 
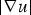$ \vert \nabla u \vert $. Our proof of the gradient estimates is based on a two-step process relying on a modified version of the Bernstein's method. As a by-product, we extend the range of applicability of the Liouville-type results known for (0.1).
