This paper is concerned with the stability issue in determining absorption and diffusion coefficients in photoacoustic imaging. Assuming that the medium is layered and the acoustic wave speed is known, we derive global Hölder stability estimates of the photoacoustic inversion. These results show that the reconstruction is stable in the region close to the optical illumination source, and deteriorate exponentially far away. Several experimental pointed out that the resolution depth of the photoacoustic modality is about tens of millimeters. Our stability estimates confirm these observations and give a rigorous quantification of this depth resolution.

Metric regularity theory lies in the very heart of variational analysis, a relatively new discipline whose appearance was, to a large extent, determined by the needs of modern optimization theory in which such phenomena as nondifferentiability and set-valued mappings naturally appear. The roots of the theory go back to such fundamental results of the classical analysis as the implicit function theorem, Sard theorem and some others. The paper offers a survey of the state of the art of some principal parts of the theory along with a variety of its applications in analysis and optimization.

Let y(h)(t,x) be one solution to \[\partial_t y(t,x) - \sum_{i, j=1}^{n}\partial_{j} (a_{ij}(x)\partial_i y(t,x))= h(t,x), \thinspace 0<t<T, \thinspace x\in \Omega\] 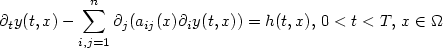with a non-homogeneous term h, and $y\vert_{(0,T)\times\partial\Omega} = 0$ 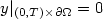,where $\Omega \subset\Bbb R^n$ 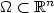is a bounded domain. We discuss an inverse problemof determining n(n+1)/2 unknown functions a ij by $\{ \partial_{\nu}y(h_{\ell})\vert_{(0,T)\times \Gamma_0}$ 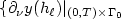, $y(h_{\ell})(\theta,\cdot)\}_{1\le \ell\le \ell_0}$ 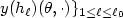after selecting input sources $h_1, ...,h_{\ell_0}$ 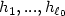suitably, where $\Gamma_0$ 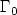is an arbitrary subboundary, $\partial_{\nu}$ 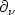denotes the normal derivative, $0 < \theta < T$ 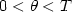and $\ell_0 \in \Bbb N$ 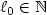. In the case of $\ell_0 = (n+1)^2n/2$ 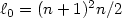, we provethe Lipschitz stability in the inverse problem if we choose $(h_1, ...,h_{\ell_0})$ 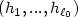from a set ${\cal H} \subset \{ C_0^{\infty}((0,T)\times \omega)\}^{\ell_0}$ 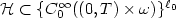with an arbitrarily fixed subdomain $\omega \subset \Omega$ 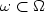. Moreover we can take $\ell_0 = (n+3)n/2$ 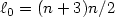by making special choices for $h_{\ell}$ 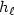, $1 \le \ell \le \ell_0$ 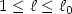. The proof is based on a Carlemanestimate.