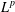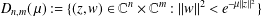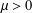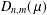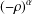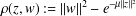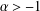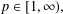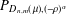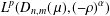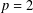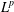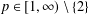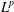The Fock–Bargmann–Hartogs domain 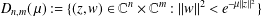 $D_{n,m}(\,\unicode[STIX]{x1D707}):=\{(z,w)\in \mathbb{C}^{n}\times \mathbb{C}^{m}:\Vert w\Vert ^{2}<e^{-\unicode[STIX]{x1D707}\Vert z\Vert ^{2}}\}$, where
$D_{n,m}(\,\unicode[STIX]{x1D707}):=\{(z,w)\in \mathbb{C}^{n}\times \mathbb{C}^{m}:\Vert w\Vert ^{2}<e^{-\unicode[STIX]{x1D707}\Vert z\Vert ^{2}}\}$, where 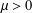 $\unicode[STIX]{x1D707}>0$, is an unbounded strongly pseudoconvex domain with smooth real-analytic boundary. We compute the weighted Bergman kernel of
$\unicode[STIX]{x1D707}>0$, is an unbounded strongly pseudoconvex domain with smooth real-analytic boundary. We compute the weighted Bergman kernel of 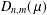 $D_{n,m}(\,\unicode[STIX]{x1D707})$ with respect to the weight
$D_{n,m}(\,\unicode[STIX]{x1D707})$ with respect to the weight 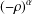 $(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}}$, where
$(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}}$, where 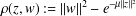 $\unicode[STIX]{x1D70C}(z,w):=\Vert w\Vert ^{2}-e^{-\unicode[STIX]{x1D707}\Vert z\Vert ^{2}}$ and
$\unicode[STIX]{x1D70C}(z,w):=\Vert w\Vert ^{2}-e^{-\unicode[STIX]{x1D707}\Vert z\Vert ^{2}}$ and 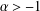 $\unicode[STIX]{x1D6FC}>-1$. Then, for
$\unicode[STIX]{x1D6FC}>-1$. Then, for 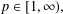 $p\in [1,\infty ),$ we show that the corresponding weighted Bergman projection
$p\in [1,\infty ),$ we show that the corresponding weighted Bergman projection 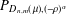 $P_{D_{n,m}(\,\unicode[STIX]{x1D707}),(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}}}$ is unbounded on
$P_{D_{n,m}(\,\unicode[STIX]{x1D707}),(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}}}$ is unbounded on 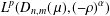 $L^{p}(D_{n,m}(\,\unicode[STIX]{x1D707}),(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}})$, except for the trivial case
$L^{p}(D_{n,m}(\,\unicode[STIX]{x1D707}),(-\unicode[STIX]{x1D70C})^{\unicode[STIX]{x1D6FC}})$, except for the trivial case 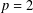 $p=2$. This gives an example of an unbounded strongly pseudoconvex domain whose ordinary Bergman projection is
$p=2$. This gives an example of an unbounded strongly pseudoconvex domain whose ordinary Bergman projection is 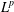 $L^{p}$ irregular when
$L^{p}$ irregular when 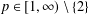 $p\in [1,\infty )\setminus \{2\}$, in contrast to the well-known positive
$p\in [1,\infty )\setminus \{2\}$, in contrast to the well-known positive 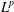 $L^{p}$ regularity result on a bounded strongly pseudoconvex domain.
$L^{p}$ regularity result on a bounded strongly pseudoconvex domain.
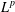 $L^{p}$ REGULARITY OF THE WEIGHTED BERGMAN PROJECTION ON THE FOCK–BARGMANN–HARTOGS DOMAIN
$L^{p}$ REGULARITY OF THE WEIGHTED BERGMAN PROJECTION ON THE FOCK–BARGMANN–HARTOGS DOMAIN