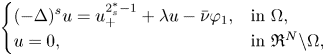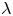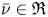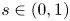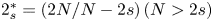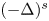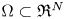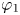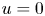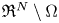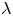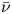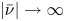4 results
On the fractional Lazer-McKenna conjecture with critical growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 879-911
- Print publication:
- August 2022
-
- Article
- Export citation
-
This paper deals with the following fractional elliptic equation with critical exponent
where
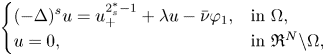\[ \begin{cases} \displaystyle (-\Delta )^{s}u=u_{+}^{2_{s}^{*}-1}+\lambda u-\bar{\nu}\varphi_{1}, & \text{in}\ \Omega,\\ \displaystyle u=0, & \text{in}\ {{\mathfrak R}}^{N}\backslash \Omega, \end{cases}\]
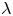$\lambda$, 
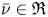$\bar {\nu }\in {{\mathfrak R}}$, 
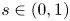$s\in (0,1)$, 
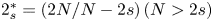$2^{*}_{s}=({2N}/{N-2s})\,(N>2s)$, 
$(-\Delta )^{s}$ is the fractional Laplace operator,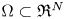 
$\Omega \subset {{\mathfrak R}}^{N}$ is a bounded domain with smooth boundary and 
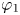$\varphi _{1}$ is the first positive eigenfunction of the fractional Laplace under the condition 
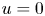$u=0$ in 
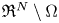${{\mathfrak R}}^{N}\setminus \Omega$. Under suitable conditions on 
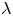$\lambda$ and 
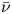$\bar {\nu }$ and using a Lyapunov-Schmidt reduction method, we prove the fractional version of the Lazer-McKenna conjecture which says that the equation above has infinitely many solutions as 
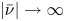$|\bar \nu | \to \infty$ .
2 - Perturbation Methods
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 54-128
-
- Chapter
- Export citation
4 - Construction of Infinitely Many Solutions
-
- Book:
- Singularly Perturbed Methods for Nonlinear Elliptic Problems
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021, pp 156-178
-
- Chapter
- Export citation
Singularly Perturbed Methods for Nonlinear Elliptic Problems
-
- Published online:
- 28 January 2021
- Print publication:
- 18 February 2021
