The subject of this paper is the problem of estimating the service time distribution of the M/G/∞ queue from incomplete data on the queue. The goal is to estimate G from observations of the queue-length process at the points of the regular grid on a fixed time interval. We propose an estimator and analyze its accuracy over a family of target service time distributions. An upper bound on the maximal risk is derived. The problem of estimating the arrival rate is considered as well.

The usual concept of asymptotic independence, as discussed in the context of extreme value theory, requires the distribution of the coordinatewise sample maxima under suitable centering and scaling to converge to a product measure. However, this definition is too broad to conclude anything interesting about the tail behavior of the product of two random variables that are asymptotically independent. Here we introduce a new concept of asymptotic independence which allows us to study the tail behavior of products. We carefully discuss equivalent formulations of asymptotic independence. We then use the concept in the study of a network traffic model. The usual infinite source Poisson network model assumes that sources begin data transmissions at Poisson time points and continue for random lengths of time. It is assumed that the data transmissions proceed at a constant, nonrandom rate over the entire length of the transmission. However, analysis of network data suggests that the transmission rate is also random with a regularly varying tail. So, we modify the usual model to allow transmission sources to transmit at a random rate over the length of the transmission. We assume that the rate and the time have finite mean, infinite variance and possess asymptotic independence, as defined in the paper. We finally prove a limit theorem for the input process showing that the centered cumulative process under a suitable scaling converges to a totally skewed stable Lévy motion in the sense of finite-dimensional distributions.

Consider an aggregate arrival process AN obtained by multiplexing N on-off processes with exponential off periods of rate λ and subexponential on periods τon. As N goes to infinity, with λN → Λ, AN approaches an M/G/∞ type process. Both for finite and infinite N, we obtain the asymptotic characterization of the arrival process activity period.

Using these results we investigate a fluid queue with the limiting M/G/∞ arrival process At∞ and capacity c. When on periods are regularly varying (with non-integer exponent), we derive a precise asymptotic behavior of the queue length random variable QtP observed at the beginning of the arrival process activity periods

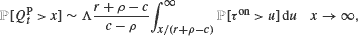
where ρ = 𝔼At∞ < c; r (c ≤ r) is the rate at which the fluid is arriving during an on period. The asymptotic (time average) queue distribution lower bound is obtained under more general assumptions regarding on periods than regular variation.

In addition, we analyse a queueing system in which one on-off process, whose on period belongs to a subclass of subexponential distributions, is multiplexed with independent exponential processes with aggregate expected rate 𝔼et. This system is shown to be asymptotically equivalent to the same queueing system with the exponential arrival processes being replaced by their total mean value 𝔼et.