We analyze asymptotically a differential-difference equation that arises in a Markov-modulated fluid model. We use singular perturbation methods to analyze the problem with appropriate scalings of the two state variables. In particular, the ray method and asymptotic matching are used.

We introduce and study a new model: zero-automatic queues. Roughly, zero-automatic queues are characterized by a special buffering mechanism evolving like a random walk on some infinite group or monoid. The salient result is that all stable zero-automatic queues have a product form stationary distribution and a Poisson output process. When considering the two simplest and extremal cases of zero-automatic queues, we recover the simple M/M/1 queue and Gelenbe's G-queue with positive and negative customers.

In this paper, motivated by the problem of the coexistence on transmission links of telecommunications networks of elastic and unresponsive traffic, we study the impact on the busy period of an M/M/1 queue of a small perturbation in the service rate. The perturbation depends upon an independent stationary process (X(t)) and is quantified by means of a parameter ε ≪ 1. We specifically compute the two first terms of the power series expansion in ε of the mean value of the busy period duration. This allows us to study the validity of the reduced service rate approximation, which consists in comparing the perturbed M/M/1 queue with the M/M/1 queue whose service rate is constant and equal to the mean value of the perturbation. For the first term of the expansion, the two systems are equivalent. For the second term, the situation is more complex and it is shown that the correlations of the environment process (X(t)) play a key role.

We consider an infinite-capacity buffer receiving fluid at a rate depending on the state of an M/M/1 queue. We obtain a new analytic expression for the joint stationary distribution of the buffer level and the state of the M/M/1 queue. This expression is obtained by the use of generating functions which are explicitly inverted. The case of a finite capacity fluid queue is also considered.

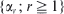An M/M/1 queue is subject to mass exodus at rate β and mass immigration at rate when idle. A general resolvent approach is used to derive occupation probabilities and high-order moments. This powerful technique is not only considerably easier to apply than a standard direct attack on the forward p.g.f. equation, but it also implicitly yields necessary and sufficient conditions for recurrence, positive recurrence and transience.

Consider a network of queues in equilibrium. When are the flows observed on two given links of that network equivalent, i.e., when do they have the same law?

The verification of the equivalence of two such point processes is first reduced to an algebraic problem by a technique based on the filtering theory.

This method is then used to show that the arrival and departure processes at an M/M/1 node in a Jackson network are not always equivalent, thereby contradicting a conjecture made in [8]. An example where that equivalence holds is also given; it provides new results on the time reversibility of some familiar processes.