We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We discuss the minimum of Willmore functional of torus in a Riemannian manifold N, especially for the case that N is a product manifold. We show that when N = S2 × S1, the minimum of W(T2) is 0, and when N = R2 × S1, there exists no torus having least Willmore functional. When N = H2(−c) × S1, and x = γ × S1, the minimum of W(x) is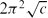 
.
