A Markov step process Z equipped with a possibly non-denumerable state space X can model a variety of queueing, communication and computer networks. The analysis of such networks can be facilitated if certain traffic flows consist of mutually independent Poisson processes with respective deterministic intensities λi (t). Accordingly, we define the multivariate counting process N = (N1, N2, · ·· Nc) induced by Z; a count in Ni occurs whenever Z jumps from x (χ into a (possibly empty) target set 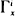. We study N through the infinitesimal operator à of the augmented Markov process W = (Z, N), and the integral relationship connecting à with the transition operator Tt of W. It is then shown that Ni depends on a non-negative function ri defined on χ; ri (x) may be interpreted as the expected rate of increase in Ni, given that Z is in state x.

A multivariate N is Poisson (i.e., composed of mutually independent Poisson streams Ni) if and only if simultaneous jumps are impossible in a certain sense, and if the conditional expectation E[ri (Z(t) | 𝒩i] = E[ri (Z(t))] for i = 1, 2, ···, c and each t ≧ 0, where 𝒩i is the σ-algebra σ{N(s), s ≦ t}. Necessary and sufficient conditions are also specified that, for each s ≦ t, the variates [Ni(t)-Ni(s)] are mutually independent Poisson distributed; this involves a weakened version of E[ri(Z(v)) | N(v) – N(u)] = E [ri(Z(v))] for i = 1, 2, ···, c and all 0 ≦ u ≦ v.

It is shown that the above criteria are automatically met by the more stringent classical requirement that N(t) and Z(t) be independent for each t ≧ 0.