1 results
On the fraction of random points by specified nearest-neighbour interrelations and degree of attraction
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 873-895
- Print publication:
- December 1987
-
- Article
- Export citation
-
Let Z1, …, Zn be i.i.d. random vectors (‘points') defined in having common density f(x) that is assumed to be continuous almost everywhere. For a fixed but otherwise arbitrary norm |.| on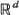
, consider the fraction Vn of those points Z1, …, Zn that are the lth nearest neighbour (with respect to |.|) to their own kth nearest neighbour, and write Sn for the fraction of points that are the nearest neighbour of exactly k other points. We derive the stochastic limits of Vn and Sn, as n tends to∞, and show how the results may be applied to the multivariate non-parametric two-sample problem.
, consider the fraction 