We show how estimators for the chain ladder prediction error in Mack's (1993) distribution-free stochastic model can be derived using the error propagation formula. Our method allows for the treatment of the general case of the prediction error of the loss development result between two arbitrary future horizons. In the well-known special cases considered previously by Mack (1993) and Merz and Wüthrich (2008), our estimators coincide with theirs. However, the algebraic form in which we cast them is new, considerably more compact and more intuitive to understand. For example, in the classical case treated by Mack (1993), we show that the mean squared prediction error divided by the squared estimated ultimate loss can be written as ∑jû2j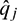 , where ûj measures the (relative) uncertainty around the jth development factor and
, where ûj measures the (relative) uncertainty around the jth development factor and 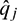 the proportion of the estimated ultimate loss that it affects. The error propagation method also provides a natural split into process error and parameter error. Our proofs identify and exploit symmetries of “chain ladder processes” in a novel way. For the sake of wider practical applicability of the formulae derived, we allow for incomplete historical data and the exclusion of outliers in the triangles.
the proportion of the estimated ultimate loss that it affects. The error propagation method also provides a natural split into process error and parameter error. Our proofs identify and exploit symmetries of “chain ladder processes” in a novel way. For the sake of wider practical applicability of the formulae derived, we allow for incomplete historical data and the exclusion of outliers in the triangles.