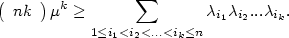The paper is motivated by the stochastic comparison of the reliabilityof non-repairable k-out-of-n systems.The lifetime of such a system with nonidentical components is compared with the lifetime of a system withidentical components.Formally the problem is as follows. Let Ui,i = 1,...,n, be positiveindependent random variables with common distribution F.For λi > 0 and µ > 0, let considerXi = Ui/λi and Yi = Ui/µ, i = 1,...,n. Remark that this is no more than a change of scale for each term.For k ∈ {1,2,...,n}, let us define Xk:n to be the kth order statistics of the random variables X1,...,Xn , andsimilarly Yk:n to be the kth order statistics ofY1,...,Yn .If Xi,i = 1,...,n, are the lifetimes of the components of an+1-k-out-of-n non-repairable system, then Xk:n is thelifetime of the system.In this paper, we give for a fixed k a sufficient condition forXk:n ≥st Yk:n where st is the usual ordering for distributions.In the Markovian case (all components have an exponential lifetime), wegive a necessary and sufficient condition.We prove that Xk:n is greater that Yk:n according to the usualstochastic ordering if and only if \[\left( \begin{array}{c} n k \end{array}\right){\mu}^k\geq \sum_{1\leqi_1<i_2<...<i_k\leq n}\lambda_{i_1}\lambda_{i_2}...\lambda_{i_k}.\]