To any finite group $\Gamma \subset {SL}_2({\mathbb {C}})$ and each element τ in the center of the group algebra of Γ, we associate a category, ${\mathcal {C}}\! oh({\mathbb {P}}^2_{_{\! \Gamma ^{\! },^{\! }\tau }},{\mathbb {P}}^1).$ It is defined as a suitable quotient of the category of graded modules over (a graded version of) the deformed preprojective algebra introduced by Crawley-Boevey and Holland. The category ${\mathcal {C}}\! oh({\mathbb {P}}^2_{_{\! \Gamma ^{\! },^{\! }\tau }},{\mathbb {P}}^1)$ should be thought of as the category of coherent sheaves on a ‘noncommutative projective space’, ${\mathbb {P}}^2_{_{\! \Gamma ^{\! },^{\! }\tau }},$ equipped with a framing at ${\mathbb {P}}^1$, the line at infinity. Our first result establishes an isomorphism between the moduli space of torsion free objects of ${\mathcal {C}}\! oh({\mathbb {P}}^2_{_{\! \Gamma ^{\! },^{\! }\tau }},{\mathbb {P}}^1)$ and the Nakajima quiver variety arising from Γ via the McKay correspondence. We apply the above isomorphism to deduce a generalization of the Crawley-Boevey and Holland conjecture, saying that the moduli space of `rank 1' projective modules over the deformed preprojective algebra is isomorphic to a particular quiver variety. This reduces, for $\Gamma =\{ 1\}$, to the recently obtained parametrisation of the isomorphism classes of right ideals in the first Weyl algebra, $\sf {A_1}$, by points of the Calogero–Moser space, due to Cannings and Holland and Berest and Wilson. Our approach is algebraic and is based on a monadic description of torsion free sheaves on ${\mathbb {P}}^2_{_{\! \Gamma ^{\! },^{\! }\tau }}$. It is totally different from the one used by Berest and Wilson, involving $\tau $-functions.
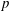 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration