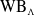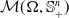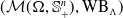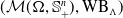1 results
On a general matrix-valued unbalanced optimal transport problem
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We introduce a general class of transport distances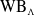
$\mathrm {WB}_{\Lambda }$ over the space of positive semi-definite matrix-valued Radon measures 
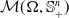$\mathcal {M}(\Omega, \mathbb {S}_+^n)$, called the weighted Wasserstein–Bures distance. Such a distance is defined via a generalised Benamou–Brenier formulation with a weighted action functional and an abstract matricial continuity equation, which leads to a convex optimisation problem. Some recently proposed models, including the Kantorovich–Bures distance and the Wasserstein–Fisher–Rao distance, can naturally fit into ours. We give a complete characterisation of the minimiser and explore the topological and geometrical properties of the space 
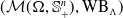$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_{\Lambda })$. In particular, we show that 
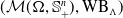$(\mathcal {M}(\Omega, \mathbb {S}_+^n),\mathrm {WB}_{\Lambda })$ is a complete geodesic space and exhibits a conic structure.
