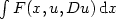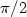We prove partial regularity with optimal Hölder exponent ofvector-valued minimizers u of the quasiconvex variational integral $\intF( x,u,Du) \,{\rm d}x$ under polynomial growth. We employ the indirectmethod of the bilinear form.

We study a variational problem which was introduced by Hannon,Marcus and Mizel [ESAIM: COCV9 (2003) 145–149] todescribe step-terraces on surfaces of so-called “unorthodox” crystals.We show that there is no nondegenerate intervals on which the absolutevalue of a minimizer is $\pi/2$ identically.

In this note we consider a stability property of p-harmonic functions in general metric measure spaces. Despite the fact that there may not be a corresponding differential equation, it is shown here that a family of uniformly convergent p-harmonic functions converges to a p-harmonic function; that is, the collection of p-harmonic functions forms a closed subspace in a certain Ho¨lder class. As a consequence, it is shown that a family of p-harmonic functions bounded in a Sobolev-type space (called the Newtonian space) has a sequence that converges locally uniformly in the domain of harmonicity to a p-harmonic function. This result is used to construct p-harmonic functions on unbounded domains. We also use this convergence result to prove a characterization of a parabolicity property of metric measure spaces. This characterization has been given for Riemannian manifolds by Holopainen, and the result here is a generalization of Holopainen's result.