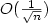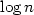1 results
Risk bounds for mixture density estimation
-
- Journal:
- ESAIM: Probability and Statistics / Volume 9 / February 2005
- Published online by Cambridge University Press:
- 15 November 2005, pp. 220-229
- Print publication:
- February 2005
-
- Article
- Export citation
-
In this paper we focus on the problem of estimating a boundeddensity using a finite combination of densities from a givenclass. We consider the Maximum Likelihood Estimator (MLE) and thegreedy procedure described by Li and Barron (1999)under the additional assumption of boundedness of densities. Weprove an $O(\frac{1}{\sqrt{n}})$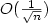
bound on the estimation errorwhich does not depend on the number of densities in the estimatedcombination. Under the boundedness assumption,this improves the bound of Li and Barron by removing the $\log n$ 
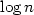factor and also generalizes it to the base classes with convergingDudley integral.
