We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We refine results of Gannon [6, Theorem 4.7] and Simon [22, Lemma 2.8] on convergence of Morley sequences. We then introduce the notion of eventual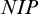
$NIP$, as a property of a model, and prove a variant of [15, Corollary 2.2]. Finally, we give new characterizations of generically stable types (for countable theories) and reinforce the main result of Pillay [17] on the model-theoretic meaning of Grothendieck’s double limit theorem.
We study nonorthogonality of symmetric, regular types and show that it preserves generic stability and is an equivalence relation on the set of all generically stable, regular types. We prove that some of the nice properties from the stable context hold in general. In the case of strongly regular types we will relate 
to the global Rudin–Keisler order.
