Many failure mechanisms can be traced to an underlying deterioration process, and stochastically changing covariates may influence this process. In this paper we propose an alternative model for assessing a system's reliability. The proposed model expresses the failure time of a system in terms of a deterioration process and covariates. When it is possible to measure deterioration as well as covariates, our model provides more information than failure time for the purpose of assessing and improving system reliability. We give several properties of our proposed model and also provide an example.

This paper studies the geometric convergence rate of a discrete renewal sequence to its limit. A general convergence rate is first derived from the hazard rates of the renewal lifetimes. This result is used to extract a good convergence rate when the lifetimes are ordered in the sense of new better than used or increasing hazard rate. A bound for the best possible geometric convergence rate is derived for lifetimes having a finite support. Examples demonstrating the utility and sharpness of the results are presented. Several of the examples study convergence rates for Markov chains.

Bounds on the tail of compound distributions are considered. Using a generalization of Wald's fundamental identity, we derive upper and lower bounds for various compound distributions in terms of new worse than used (NWU) and new better than used (NBU) distributions respectively. Simple bounds are obtained when the claim size distribution is NWUC, NBUC, NWU, NBU, IMRL, DMRL, DFR and IFR. Examples on how to use these bounds are given.

We examine a continuous search model in which rewards (e.g. job offers in a search model in the labor market, price offers for a given asset, etc.) are received randomly according to a renewal process determined by a known distribution function. The rewards are non-negative independent and have a common distribution with finite mean. Over the search period there is a constant cost per unit time. The searcher's objective is to choose a stopping time at which he receives the highest available reward (offer), so as to maximize the net expected discounted return. If the interarrival time distribution in the renewal process is new better than used (NBU), it is shown that the optimal stopping strategy possesses the control limit property. The term ‘control limit policy' refers to a strategy in which we accept the first reward (offer) which exceeds a critical control level ξ.

A probability measure μ on ℝn+ is defined to be strongly new better than used (SNBU) if 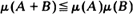for all increasing subsets . For n = 1 this is equivalent to being new better than used (NBU distributions play an important role in reliability theory). We derive an inequality concerning products of NBU probability measures, which has as a consequence that if μ1, μ2, ···, μn are NBU probability measures on ℝ+, then the product-measure μ = μ × μ2 × ··· × μn on ℝn+ is SNBU. A discrete analog (i.e., with N instead of ℝ+) also holds.

Applications are given to reliability and percolation. The latter are based on a new inequality for Bernoulli sequences, going in the opposite direction to the FKG–Harris inequality. The main application (3.15) gives a lower bound for the tail of the cluster size distribution for bond-percolation at the critical probability. Further applications are simplified proofs of some known results in percolation. A more general inequality (which contains the above as well as the FKG-Harris inequality) is conjectured, and connections with an inequality of Hammersley [12] and others ([17], [19] and [7]) are indicated.

In this paper we define and analyze a class of cumulative shock models associated with a bivariate sequence {Xn, Yn}∞n=0 of correlated random variables. The {Xn} denote the sizes of the shocks and the {Yn} denote the times between successive shocks. The system fails when the cumulative magnitude of the shocks exceeds a prespecified level z. Two models, depending on whether the size of the nth shock is correlated with the length of the interval since the last shock or with the length of the succeeding interval until the next shock, are considered. Various transform results and asymptotic properties of the system failure time are obtained. Further, sufficient conditions are established under which system failure time is new better than used, new better than used in expectation, and harmonic new better than used in expectation.

In this paper we study some distribution properties of the system failure time in general shock models associated with correlated renewal sequences (Xn, Yn) . Two models, depending on whether the magnitude of the nth shock Xn is correlated to the length Yn of the interval since the last shock, or to the length of the subsequent interval to the next shock, are considered. Sufficient conditions under which the system failure time is completely monotone, new better than used, new better than used in expectation, and harmonic new better than used in expectation are given for these two models.

This paper extends results of Esary, Marshall and Proschan (1973) and A-Hameed and Proschan (1973). We consider the life distribution of a device subject to a sequence of shocks occurring randomly in time according to a nonstationary pure birth process: given k shocks have occurred in [0, t], the probability of a shock occurring in (t, t + Δ] is λ kλ (t)Δ + o (Δ). We show that various fundamental classes of life distributions (such as those with increasing failure rate, or those with the ‘new better than used' property, etc.) are obtained under appropriate assumptions on λ k, λ (t), and on the probability of surviving a given number of shocks.