The main objective of this paper is to address the following question: are the containment measures imposed by most of the world governments effective and sufficient to stop the epidemic of COVID-19 beyond the lock-down period? In this paper, we propose a mathematical model which allows us to investigate and analyse this problem. We show by means of the reproductive number, ${\cal R}_0$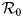 that the containment measures appear to have slowed the growth of the outbreak. Nevertheless, these measures remain only effective as long as a very large fraction of population, p, greater than the critical value $1-1/{\cal R}_0$ 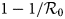remains confined. Using French current data, we give some simulation experiments with five scenarios including: (i) the validation of model with p estimated to 93%, (ii) the study of the effectiveness of containment measures, (iii) the study of the effectiveness of the large-scale testing, (iv) the study of the social distancing and wearing masks measures and (v) the study taking into account the combination of the large-scale test of detection of infected individuals and the social distancing with linear progressive easing of restrictions. The latter scenario was shown to be effective at overcoming the outbreak if the transmission rate decreases to 75% and the number of tests of detection is multiplied by three. We also noticed that if the measures studied in our five scenarios are taken separately then the second wave might occur at least as far as the parameter values remain unchanged.

This article argues for a departure from theories of new cinema “waves” and proposes the notion of cinema “winds” as a more compelling conceptual framework for studies of African film movements. Building on the work of Ngũgĩ wa Thiong’o, Manthia Diawara, Ken Harrow, and Nwachukwu Frank Ukadike, in addition to commentaries by various African film directors, this article looks at various dimensions of global visibility and the elusive movements of African cinemas. It also explores how African directors challenge habits of seeing and interpreting world cinema.