We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article we study integral models of Shimura varieties, called Pappas–Rapoport splitting model, for ramified P.E.L. Shimira data. We study the special fiber and some stratification of these models, in particular we show that these are smooth and the Rapoport locus and the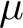 
$\mu $-ordinary locus are dense, under some condition on the ramification.
