Increasing penetration of variable and intermittent renewable energy resources on the energy grid poses a challenge for reliable and efficient grid operation, necessitating the development of algorithms that are robust to this uncertainty. However, standard algorithms incorporating uncertainty for generation dispatch are computationally intractable when costs are nonconvex, and machine learning-based approaches lack worst-case guarantees on their performance. In this work, we propose a learning-augmented algorithm, RobustML, that exploits the good average-case performance of a machine-learned algorithm for minimizing dispatch and ramping costs of dispatchable generation resources while providing provable worst-case guarantees on cost. We evaluate the algorithm on a realistic model of a combined cycle cogeneration plant, where it exhibits robustness to distribution shift while enabling improved efficiency as renewables penetration increases.
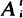 , where the components of
, where the components of 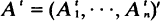 are independent renewal processes, with
are independent renewal processes, with 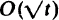 and if λ is exterior to Λ it grows as
and if λ is exterior to Λ it grows as 