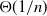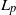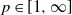We introduce a general two-colour interacting urn model on a finite directed graph, where each urn at a node reinforces all the urns in its out-neighbours according to a fixed, non-negative, and balanced reinforcement matrix. We show that the fraction of balls of either colour converges almost surely to a deterministic limit if either the reinforcement is not of Pólya type or the graph is such that every vertex with non-zero in-degree can be reached from some vertex with zero in-degree. We also obtain joint central limit theorems with appropriate scalings. Furthermore, in the remaining case when there are no vertices with zero in-degree and the reinforcement is of Pólya type, we restrict our analysis to a regular graph and show that the fraction of balls of either colour converges almost surely to a finite random limit, which is the same across all the urns.

It is well-known that in a small Pólya urn, i.e., an urn where the second largest real part of an eigenvalue is at most half the largest eigenvalue, the distribution of the numbers of balls of different colours in the urn is asymptotically normal under weak additional conditions. We consider the balanced case, and then give asymptotics of the mean and the covariance matrix, showing that after appropriate normalization, the mean and covariance matrix converge to the mean and covariance matrix of the limiting normal distribution.

Consider a Pólya urn with balls of several colours, where balls are drawn sequentially and each drawn ball is immediately replaced together with a fixed number of balls of the same colour. It is well known that the proportions of balls of the different colours converge in distribution to a Dirichlet distribution. We show that the rate of convergence is $\Theta(1/n)$ in the minimal $L_p$ metric for any $p\in[1,\infty]$, extending a result by Goldstein and Reinert; we further show the same rate for the Lévy distance, while the rate for the Kolmogorov distance depends on the parameters, i.e. on the initial composition of the urn. The method used here differs from the one used by Goldstein and Reinert, and uses direct calculations based on the known exact distributions.