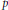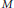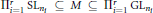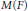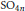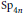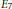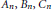For a unitary unramified genuine principal series representation of a covering group, we study the associated R-group. We prove a formula relating the R-group to the dimension of the Whittaker space for the irreducible constituents of such a principal series representation. Moreover, for certain saturated covers of a semisimple simply connected group, we also propose a simpler conjectural formula for such dimensions. This latter conjectural formula is verified in several cases, including covers of the symplectic groups.

Let $F$ be a 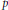$p$-adic field of characteristic 0, and let 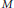$M$ be an $F$-Levi subgroup of a connected reductive $F$-split group such that 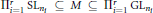$\Pi _{i=1}^{r}\,\text{S}{{\text{L}}_{ni}}\,\subseteq \,M\,\subseteq \,\Pi _{i=1}^{r}\,\text{G}{{\text{L}}_{ni}}$ for positive integers $r$ and ${{n}_{i}}$. We prove that the Plancherel measure for any unitary supercuspidal representation of 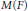$M\left( F \right)$ is identically transferred under the local Jacquet–Langlands type correspondence between 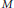$M$ and its $F$-inner forms, assuming a working hypothesis that Plancherel measures are invariant on a certain set. This work extends the result of Muić and Savin (2000) for Siegel Levi subgroups of the groups 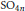$\text{S}{{\text{O}}_{4n}}$ and 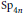$\text{S}{{\text{p}}_{4n}}$ under the local Jacquet–Langlands correspondence. 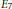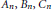It can be applied to a simply connected simple $F$-group of type ${{E}_{6}}$ or ${{E}_{7}}$, and a connected reductive $F$-group of type ${{A}_{n}},\,{{B}_{n}},\,{{C}_{n}}$ or ${{D}_{n}}$.

An affine Hecke algebra $\mathcal{H}$ contains a large abelian subalgebra $\mathcal{A}$ spanned by the Bernstein–Zelevinski–Lusztig basis elements $\theta_x$, where $x$ runs over (an extension of) the root lattice. The centre $\mathcal{Z}$ of $\mathcal{H}$ is the subalgebra of Weyl group invariant elements in $\mathcal{A}$. The natural trace (‘evaluation at the identity’) of the affine Hecke algebra can be written as integral of a certain rational $n$-form (with values in the linear dual of $\mathcal{H}$) over a cycle in the algebraic torus $T=\textrm{Spec}(\mathcal{A})$. This cycle is homologous to a union of ‘local cycles’. We show that this gives rise to a decomposition of the trace as an integral of positive local traces against an explicit probability measure on the spectrum $W_0\setminus T$ of $\mathcal{Z}$. From this result we derive the Plancherel formula of the affine Hecke algebra.

AMS 2000 Mathematics subject classification: Primary 20C08; 22D25; 22E35; 43A32

The main goal of this Letter is to give a new proof of a result conjectured by D. De George and N. Wallach and proved by P. Delorme and to extend it to the $S$-arithmetic setting. The proof is based on a density principle.